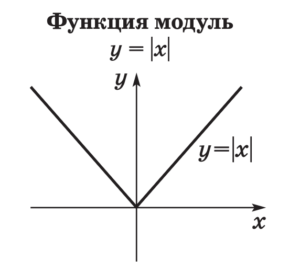
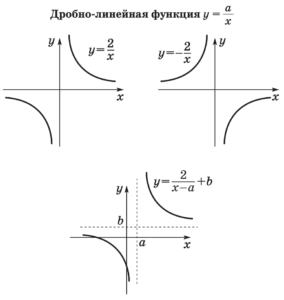
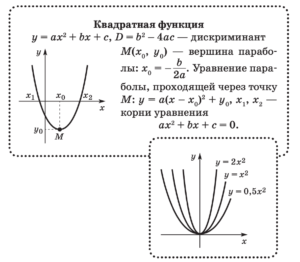
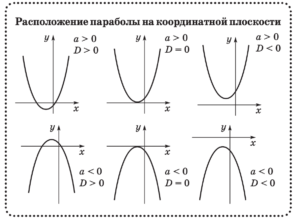
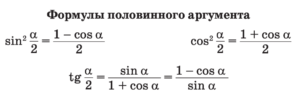
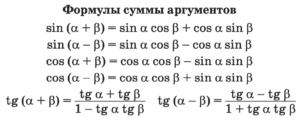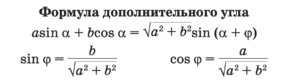- Событие — это явление, о котором можно сказать, что оно происходит или не происходит при определенных условиях.
- Испытания — это условия, в результате которых происходит (или не происходит) событие.
- Случайным называется событие, которое может произойти или не произойти во время проведения определенного испытания. Например: во время вытягивания наугад одной карты из колоды вы взяли даму.
- Массовыми называют однородные события, наблюдающиеся при определенных условиях, которые могут быть повторены неограниченное количество раз. Например, попадание или промах в серии выстрелов; появление бракованных деталей при серийном выпуске и др.
- Достоверным называется событие, которое вследствие данного испытания обязательно произойдет. Например, событие «появление на одной из граней игрального кубика натурального числа меньше7» является достоверным.
- Невозможным называется событие, которое вследствие данного испытания не может произойти. Например, событие «появление на одной из граней игрального кубика числа 7» является невозможным.
- Попарно несовместимые события — это события, два из которых не могут произойти одновременно. Например, попадание и промах при одном выстреле.
- Равновозможные события — это такие события, каждое из которых не имеет никаких преимуществ в появлении чаще, чем другое, во время многоразовых испытаний, которые проводятся при одинаковых условиях. Например, появление чисел 1, 2, 3, 4, 5, 6 при броске игрального кубика –равновозможные события.
Классическое определение вероятности
Отношение числа событий, которые способствуют событию А, к общему количеству событий пространства элементарных событий, называются вероятностью случайного события А и обозначается Р(А).
Формула нахождения вероятности
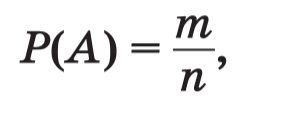
где A — событие; P(A) — вероятность события; n число всех возможных элементарных событий; m число событий, которые способствуют событию А.
Теоремы о вероятностях событий
Вероятность произведения
Теорема: вероятность произведения двух независимых событий A и B равна произведению этих вероятностей:
P(AB) = P(A) · P(B).
Произведением событий A и B называется событие C = A · B, состоящее в том, что в результате испытания произошло и событие A, и событие B, т.е. оба события произошли. Два события A и B называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события A и B называются зависимыми.
Сложение вероятностей
Теорема: вероятность суммы двух несовместных событий A и B равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B) .
Суммой событий A и B называется событие C = A + B, состоящее в наступлении, по крайней мере, одного из событий A или B, т. е. в наступлении события A, или события B, или обоих этих событий вместе, если они совместны.
Условная вероятность
Пусть A и B — зависимые события. Условной вероятностью PA (B) события B называется вероятность события B, найденная в предположении, что событие A уже наступило.
Теорема: вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило:

Теорема: вероятность суммы двух совместных событий A и B равна сумме вероятностей этих событий минус вероятность их произведения:
P(A + B) + P(A) + P(B) – P(AB).
Примеры заданий:
Задание №31. В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того. что Аня и Нина окажутся в одной группе.
Решение.
Пусть Аня оказалась в некоторой группе. Тогда для 20 оставшихся учащихся оказаться с ней в одной группе есть две возможности. Вероятность этого события равна 2 : 20 = 0,1.
Ответ: 0,1
Задание №32. В кармане у Миши было четыре конфеты — «Грильяж», «Белочка», «Коровка» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».
Решение.
В кармане было 4 конфеты, а выпала одна конфета. Поэтому вероятность этого события равна одной четвертой.
Ответ: 0,25.
Задание №33. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «А = сумма очков равна 5»?
Решение.
Сумма очков может быть равна 5 в четырех случаях: «3 + 2», «2 + 3», «1 + 4», «4 + 1».
Ответ: 4.
Задание №34. В коробке вперемешку лежат чайные пакетики с чёрным и зелёным чаем, одинаковые на вид, причём пакетиков с чёрным чаем в 19 раз больше, чем пакетиков с зелёным. Найдите вероятность того, что случайно выбранный из этой коробки пакетик окажется пакетиком с зелёным чаем.
Решение.
Пусть количество пакетиков с зелёным чаем равно x, тогда пакетиков с чёрным чаем 19x, а всего 20x. Значит, вероятность того, что случайно выбранный пакетик окажется пакетиком с зелёным чаем, равна
x = 0,05*20x
Ответ: 0,05.
Задание №35. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решение.
Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 –0,8 = 0,2. Событие попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся»
равна: 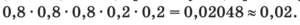
Ответ: 0,02.
Задание №36. Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 45% этих стёкол, вторая — 55%. Первая фабрика выпускает 3% бракованных стёкол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение.
Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,45 · 0,03 = 0,0135.
Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,55 · 0,01 = 0,0055. Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным, равна 0,0135 + 0,0055 = 0,019.
Ответ: 0,019.
Задание №37. Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решение.
Пусть A = «чайник прослужит больше года, но меньше двух лет», B = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года». События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду, — равна нулю. Тогда:
P(A + B+ С) = P(A) + P(B)+ P(С)= P(A) + P(B),откуда, используя данные из условия, получаем: 0,97 = P(A) + 0,89. Тем самым, для искомой вероятности имеем: P(A) = 0,97 − 0,89 = 0,08.
Ответ: 0,08.
Задание №38. Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.
Решение.
Рассмотрим события A = «учащийся решит 11 задач» и В = «учащийся решит больше 11 задач». Их сумма — событие A + B = «учащийся решит больше 10 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем:
0,74 = P(A) + 0,67, откуда P(A) = 0,74 − 0,67 = 0,07.
Ответ: 0,07.
Задание №39. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.
Решение.
Ситуация, при которой батарейка будет забракована, может сложиться в результате событий: A батарейка действительно неисправна и забракована справедливо или В — батарейка исправна, но по ошибке забракована. Это несовместные события, вероятность их суммы равна сумме вероятностей эти событий. Имеем:
P(A + B) + P(A) + P(B) + 0,02 · 0,99 + 0,98 · 0,01 =0,0198 + 0,0098 = 0,0296.
Ответ: 0,0296.

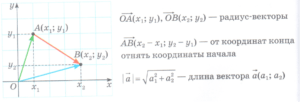
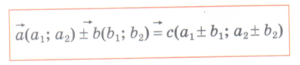
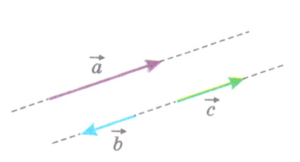 Коллинеарными векторами называют векторы, которые лежат на параллельных прямых или на одной прямой.
Коллинеарными векторами называют векторы, которые лежат на параллельных прямых или на одной прямой. ![]()

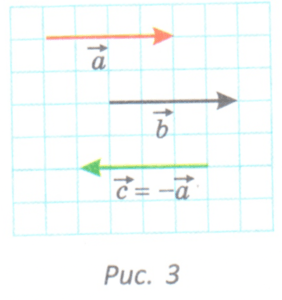




















 Скалярный квадрат вектора равен квадрату его длины.
Скалярный квадрат вектора равен квадрату его длины.


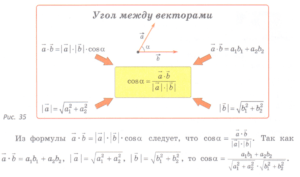



![]()









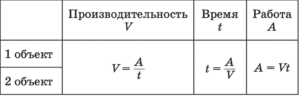








 Задание №19. Из пункта A круговой трассы выехал велосипедист. Через 30 минут он ещё не вернулся в пункт А, и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Задание №19. Из пункта A круговой трассы выехал велосипедист. Через 30 минут он ещё не вернулся в пункт А, и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.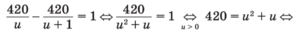










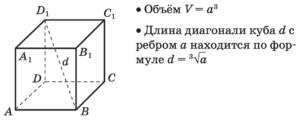



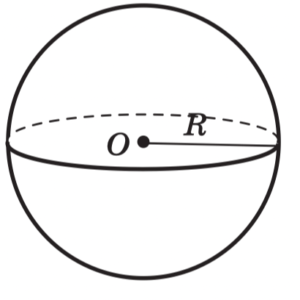 Шар
Шар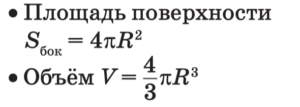
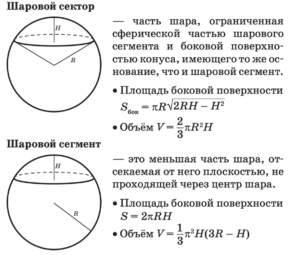
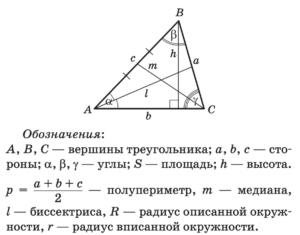

 Площадь треугольника
Площадь треугольника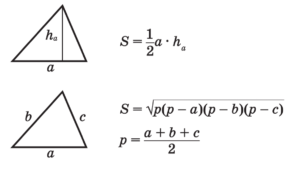
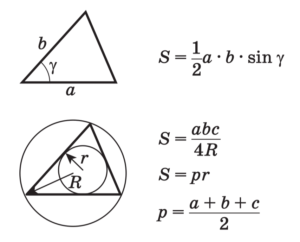
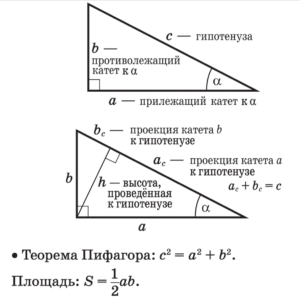
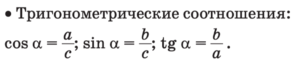

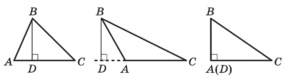
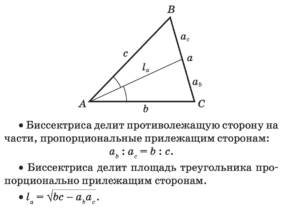
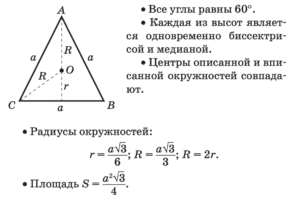 Медиана, биссектриса,
Медиана, биссектриса,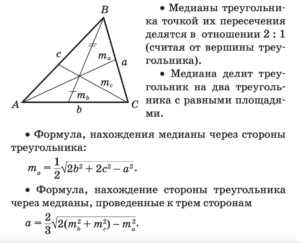
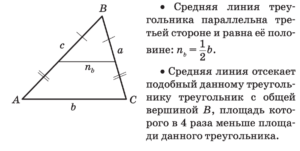

 Квадрат
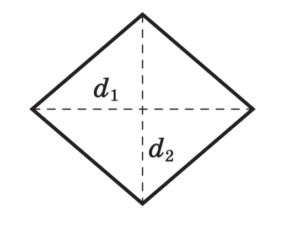
Квадрат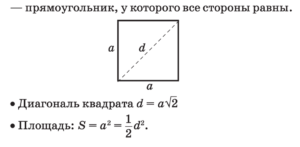 Трапеция
Трапеция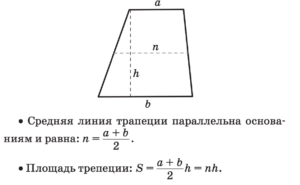
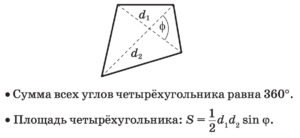 Произвольный выпуклый многоугольник
Произвольный выпуклый многоугольник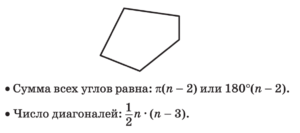
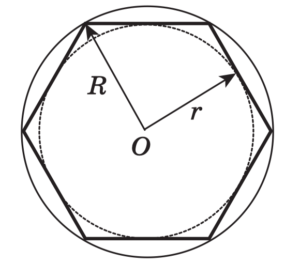
 Окружность
Окружность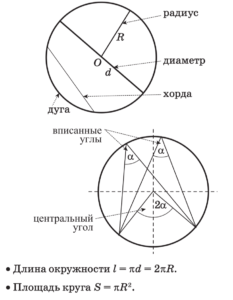 Свойства хорды
Свойства хорды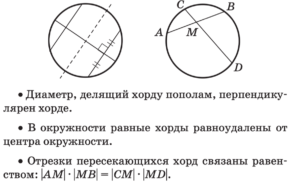
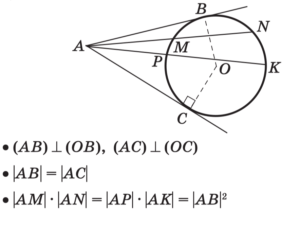

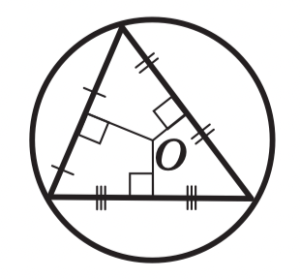 Центр окружности, описанной около треугольника
Центр окружности, описанной около треугольника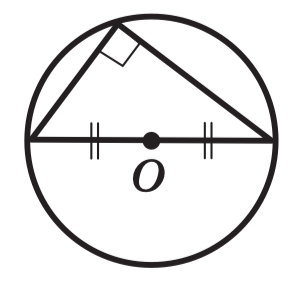 Центр окружности, описанной около
Центр окружности, описанной около