Привет, с вами репетитор по математике. Своим ученикам я всегда говорю, что математика- это воздушный шар, чем больше выбросишь ненужного из корзины, тем легче и выше будет полёт.
При вычислениях, преобразованиях и упрощениях выражений полезно следовать следующим рекомендациям:
- — упростите выражение: вынесите общий множитель за скобки, приведите подобные слагаемые;
- не торопитесь перемножать числа в числители и знаменатели, вот увидите, обязательно что-нибудь да сократится;
- всегда ищите НАИМЕНЬШИЙ общий знаменатель, для этого сначала разложите все знаменатели на множители, из первого выберите ВСЕ, из остальных — НЕДОСТАЮЩИЕ, и НЕ ПЕРЕМНОЖАЙТЕ;
- при работе с дробями всегда переводите их к ОДНОМУ виду: при сложении и вычитании удобнее работать с десятичными дробями, при умножении и делении — с обыкновенными;
- НИКОГДА не работайте со смешанными дробями, лучше переходите к обыкновенной дроби (5¾=5+¾=23/4). Если числа слишком большие запишите смешанную дробь в виде суммы целой и дробной части, т.е. целого числа и обыкновенной дроби:
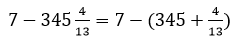
- Помните, что
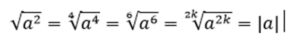 степень корня — чётная.
степень корня — чётная.
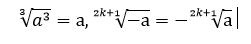 степень корня — нечетная.
степень корня — нечетная.
При работе с последовательностями и натуральными числами совсем нелишним будет:
- выписать все члены последовательности (если их меньше 20, до фанатизма доходить не нужно) или хотя бы первые 4-5 членов и последние 3-4. Пример:
В арифметической прогрессии 1-й член равен 11, разность прогрессии равна -3, а сумма всех членов прогрессии равна 4. Сколько членов в этой прогрессии? (Варианты ответов: 1)7; 2)8; 3)9; 4)10; 5)11.
Решение: Для решения этой задачи, как, впрочем, и для большинства задач про прогрессию, достаточно знать определение арифметической прогрессии: каждый следующий член равен предыдущему плюс разность прогрессии. Значит, второй член — это 11+(-3)=8, третий — это 8+(-3) = 5 и т.д.
Начинаем суммировать. Сначала 7 слагаемых (первый вариант ответа):
11+8+5+2+(-1)+(-4)+(-7)=14.
Ответ не подошел, добавляем еще слагаемое, и получаем нужную нам сумму. Значит, верный ответ — второй. Ответ: 2.
При решении уравнений и неравенств:
- где только возможно — рисуй. Используй свойства функций (монотонность, четность-нечетность, ограниченность);
- не забывай про ОДЗ и условия, при которых задача может иметь решения. Часто это позволяет упростить условие и решение задачи;
- помни, что преимущество уравнений в том, что всегда можно сделать проверку, подставив полученные значения переменной. Но делать это нужно только с ПЕРВОНАЧАЛЬНЫМ условием;
- никогда не «сокращай» одинаковые множители в обеих частях уравнения или неравенства, при этом можно потерять корни. И проверка не поможет. Лучше вынести общий множитель за скобки и проанализировать полученное произведение.
Решая геометрические задачи, помни, что:
- правильный чертёж — половина решения задачи;
- первый чертёж позволяет только увидеть общую картину взаимного расположения объектов. Уточняй чертёж до тех пор, пока четко не увидишь ситуацию.
- при построении чертежа вместо линейки, которой не разрешено пользоваться (вот жадины), используй край паспорта (гражданина РБ). Высоты стройте с помощью уголка листа;
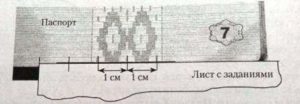 . А вы не знали?
. А вы не знали?
- обозначать данные и уже найденные элементы нужно прямо на чертеже;
- 3,4,5 5,12,13 8,15,17 7,24,25 — пифагоровы тройки, знание которых сэкономит время при нахождении элементов прямоугольных треугольников;
- любой отрезок, перпендикулярный стороне прямоугольного треугольника, образует треугольник, подобных исходному (убедитесь уже сами).
Ваш репетитор по математике.
Кстати, если у вас еще нет блога, то вы можете создать его всего за 3 занятия в бесплатной онлайн-школе Евгения Вергуса


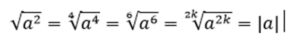 степень корня — чётная.
степень корня — чётная. . А вы не знали?
. А вы не знали?