Векторы

Вектор — направленный отрезок, т.е. отрезок, один которого принимается за начало, другой — за конец вектора.

Координаты векторы

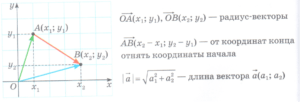
Сложение (вычитание) векторов, заданных координатами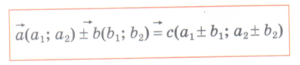

Коллинеарные векторы

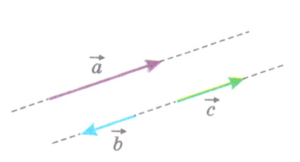Коллинеарными векторами называют векторы, которые лежат на параллельных прямых или на одной прямой.

Коллинеарные векторы, которые направлены в одну сторону, называются сонаправленными, а коллинеарные векторы, направленные в противоположные стороны, — противоположно направленными векторами. 

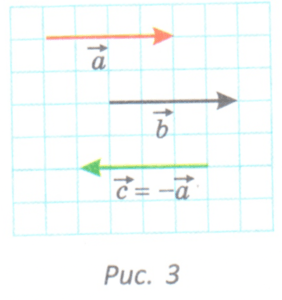
Равными векторами называются два вектора, которые равны по длине и совпадают по направлению. Противоположными векторами называются два вектора, которые равны по длине, но противположны по направлению. Вектор,

Замечание: следует различать понятия «равные векторы» и «векторые, равные по длине». Равные по длине векторы могут отличаться по направлению. Также следует различать понятия «противоположные векторы», которые равные по длине, и «противоположно направленные векторы», которые могут отличаться по длине.

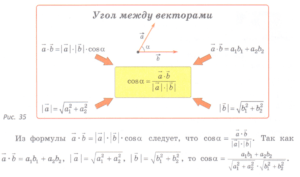
Угол между векторами

Углом между векторами называется угол между векторами, коллинеарными данным и отложенными от одной точки.

Действия над векторами

Умножение вектора на число

Сложение векторов

Вычитание векторов

Координаты вектора

Разложение вектора по двум неколлинеарным векторам

Координаты вектора в прямоугольной системе координат

Равные векторы имеют равные одноимённые координаты, т. е. равные первые и  равны вторые координаты. Это объясняется тем, что любой из множества равных векторов, будучи отложенным от начала координат, совпадёт с равным ему радиус-вектором (от точки вектор, равный данному, можно отложить единственным способом), т.е. он будет иметь такие же координаты, как и этот радиус-вектор.

Действия над векторами, заданными своими координатами

Коллинеарность векторов, заданных координатами

Координаты вектора, заданного координатами его начала и конца

Длина вектора, заданного координатами

Скалярное произведение векторов

Скалярное произведение векторов, заданных направленными отрезками

Скалярный квадрат вектора равен квадрату его длины.

Свойства скалярного произведения

Скалярное произведение векторов,
заданных координатами

Координатно-векторный метод
решения задач

Координатный метод

Введение системы координат при решении геометрических задач позволяет перевести эти задачи на язык алгебры и свести их решение многих задач, привлекая к решению модный алгебраический аппарат.

Пример 1. Доказать, что в прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы.

Пример 2. Доказать, что если расстояние от прямой до центра окружности меньше её радиуса, то прямая имеет с окружностью две общие точки, если это расстояние равно радиусу, то — одну общую точку, если больше радиуса — ни одной.

Векторный метод

Введение векторов при решении геометрических задач позволяет перевести их решение на язык действий с векторами. Такой метод решения задач называется векторным. Иногда векторный метод значительно упрощает решение задачи. Например, доказательство того, что некоторые точки А, В и С лежат на одной прямой традиционным способом довольно трудоёмкое. Однако оно может быть сведено к доказательству того, что

Пример 3. Доказать, что средняя линия треугольника параллельна основанию и равна его половине.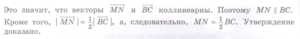
Пример 4. Доказать, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.