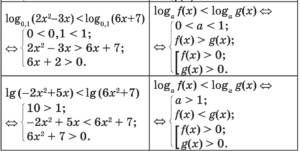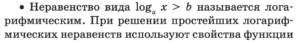Неравенства

Разберём алгоритмы решения несложных рациональных, показательных и логарифмических неравенств и задачи на сравнение чисел с помощью свойств числовых неравенств. Для этого достаточно уметь решать линейные и квадратные неравенства, а также простейшие дробно-рациональные, показательные и логарифмические неравенства, применять свойства числовых неравенств, прикидки и оценки к сравнению чисел.

СОВЕТ

Эти умения вам понадобятся при решении рациональных, показательных или логарифмических неравенств, их систем либо задач на сравнение чисел с помощью свойств числовых неравенств на базовом уровне. 

Если в условии задания есть неравенство, в решении которого вы сомневаетесь, то оставьте его на потом. Сначала решите те неравенства, которые вы можете решить, и установите соответствие между этими неравенствами и их решениями. И тогда оставшееся решение будет соотноситься с тем неравенством, в решении которого вы сомневаетесь.

ЗАМЕЧАНИЯ

• Допустимые значения неизвестных (ОДЗ) неравенства не обязательно удовлетворяют неравенству, но решения неравенства обязательно входят в ОДЗ.
• Преобразование входящих в неравенства выражений не должно сужать ОДЗ, так как могут быть потеряны решения неравенств.
• Преобразование входящих в неравенства выражений не должно расширять ОДЗ, так как могут быть приобретены лишние решения неравенств. В случае расширения ОДЗ надо сразу вводить необходимые ограничения на неизвестную величину.
  

  Решение неравенств

  Решение неравенств основано на теоремах равносильности неравенств:

Алгебраические неравенства

Рациональные неравенства:
(обычно решают методом интервалов)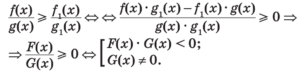

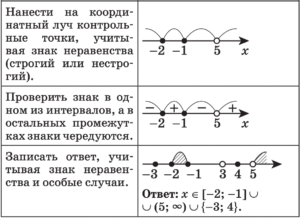
ЗАМЕЧАНИЕ

• Справа и слева от контрольных точек, полученных из линейных множителей чётной степени, приравнивая их к нулю, знак не меняется.
• Точки, которые не входят в интервал, но в них неравенство выполняется, записываются в ответе в фигурных скобках.
• Все контрольные точки на схеме отмечаются закрашенными точками, и в ответе интервал записан в квадратных скобках, так как знак сравнения неравенства нестрогий (меньше и равно — это нестрогий знак).

ЗАМЕЧАНИЕ

Все контрольные точки на схеме отмечаются незакрашенными точками и в ответе интервал записан в круглых скобках, так как знак сравнения неравенства строгий.

  ПРИМЕРЫ ЭКЗАМЕНАЦИОННЫХ ЗАДАНИЙ

ЗАМЕЧАНИЕ

На схеме числовые значения контрольных точек, которые получены из скобок чётной степени, подчёркнуты.

Иррациональные неравенства

Решение иррациональных неравенств сводится к решению равносильных неравенств, при этом:

Показательные и логарифмические неравенства

Показательное неравенство

Логарифмическое неравенство

Свойства неравенств:

Примеры заданий показательных неравенств и формулы, необходимые для их решения
Доведите решение до ответа самостоятельно.

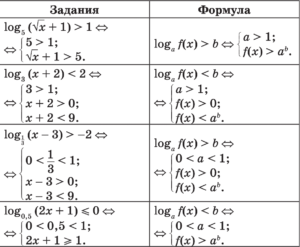
Примеры заданий логарифмических неравенств и формулы, необходимые для их решения

Доведите решение до ответа самостоятельно.