Текстовые задачи

Текстовые задачи условно можно разбить на следующие основные группы:

• задачи на части и проценты; x задачи с целочисленными данными;
• задачи на движение;
• задачи на сплавы, растворы и смеси;
• задачи на работу.

Методы решения этих задач имеют много общего и одновременно некоторые специфические особенности.

Алгоритм решения текстовых задач

• Ввод переменных, т. е. обозначение буквами x, y, z… величины, которые требуется найти по условию задачи.
• Перевод условий задачи на язык математических соотношений, т. е. составление уравнений, неравенств, введение ограничения.
• Решение уравнений или неравенств.
• Проверка полученных решений на выполнение условий задачи.

Указания к решению текстовых задач

• Набор неизвестных должен быть достаточным для перевода условий задачи на язык математических соотношений. Как правило, за неизвестные следует принимать искомые величины.
• Выбрав неизвестные, в процессе перевода условий задачи в уравнения или неравенства необходимо использовать все данные и условия задачи.
• При составлении уравнений или неравенств необходимо исходить из требования о решении задачи в общем виде.
• В составленных уравнениях надо проверить размерность членов уравнений
• В процессе решения задачи надо избегать результатов, противоречащих физическому смыслу.

Задачи на части и проценты

Основные задачи на части и проценты

• нахождение данной части числа; x нахождение числа по заданной его части;
• нахождение процентного отношения двух чисел;
• нахождение наращенного капитала (сложные проценты) при заданной процентной ставке (т. е. процент прироста капитала);
• нахождение времени, в течение которого капитал возрастает.

Задачи на части

При решении этого типа задач основным понятием является часть числа. Если задана величина а, то её k-я часть равна kа, где k > 0.

Задачи на проценты

Основные типы задач на проценты

Задачи на выполнение определённого объёма работы

При решении задач, связанных с выполнением определённого объёма работ, используют следующие соотношения:

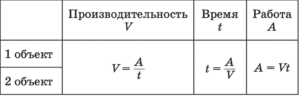
Задачи на движение

При решении задач на движение принимают такие допущения:

• движение считается равномерным, если нет специальных оговорок;

• изменение направления движения и переходы на новый режим движения считаются происходящими мгновенно;Задание №19. Из пункта A круговой трассы выехал велосипедист. Через 30 минут он ещё не вернулся в пункт А, и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.

  Решение.

  К моменту первого обгона мотоциклист за 10 минут проехал столько же, сколько велосипедист за 40 минут, следовательно, его скорость в 4 раза больше. Поэтому, если скорость велосипедиста принять за x км/час, то скорость мотоциклиста будет равна 4x, а скорость их сближения — 3x км/час.

  C другой стороны, второй раз мотоциклист догнал велосипедиста за 30 минут, за это время он проехал на 30 км больше. Следовательно, скорость их сближения составляет 60 км/час.

  Итак, 3х = 60 км/час, откуда скорость велосипедиста равна 20 км/час, а скорость мотоциклиста равна 80 км/час.

  Ответ: 80.

  Задание №20. От пристани A к пристани B, расстояние между которыми равно 420 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним, со скоростью на 1 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.

  Решение.

  Пусть u км/ч — скорость первого теплохода, тогда скорость второго теплохода по течению равна u + 1 км/ч. Первый теплоход находился в пути на 1 час больше, чем второй, отсюда получаем:

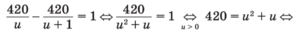
Задачи на сплавы, растворы и смеси

При решении задач этого типа используются следующие допущения:

• Все полученные сплавы, растворы, смеси считаются однородными.
• При соединении растворов и сплавов не учитываются химические взаимодействия их отдельных компонентов.
• Считают, что литр как мера вместимости сосуда равен литру как меры количества жидкости.
• Если два сплава (раствора) соединяют в один «новый» сплав (раствор), то выполняются равенства:
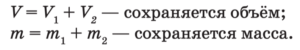
• Если первый сплав состоит из нескольких компонентов, например из А, В, С, а второй — из компонентов В, С, D, то «новый» сплав, полученный при соединении этих двух сплавов, будет содержать компоненты А, В, С, D, причём массы этих компонентов в «новом» сплаве равны сумме масс каждого из компонентов, входящих в первый и второй сплавы. 

Очень часто в задачах на смеси и сплавы используются понятия объёмной концентрации и массовой концентрации компонентов, составляющих раствор или сплав. Объёмная (массовая) концентрация есть число, показывающее, какую долю всего объёма (массы) составляет данный компонент.

Алгоритм решения задачи на сплавы, растворы и смеси:

• Изучить условия задачи. Выбрать неизвестные величины (их обозначают буквами х, у и т.д.), относительно которых составить пропорции. Этим мы создаём математическую модель ситуации, описанной в условии задачи.
• Используя условия задачи, определить все взаимосвязи между данными величинами.
• Составить математическую модель задачи и решить её.
• Изучить полученное решение, провести критический анализ результата.

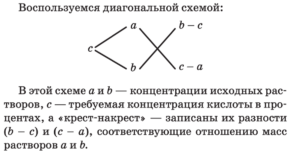
Задание №22. Имеется два сплава. Первый содержит 15% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 140 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

Решение.

Пусть масса первого сплава m 1 кг, а масса второго — m 2 кг. Тогда массовое содержание никеля в первом и втором сплавах 0,15m 1 и 0,35m 2 соответственно. Из этих двух сплавов получили третий сплав массой 140 кг, содержащий 30% никеля. Получаем систему уравнений: