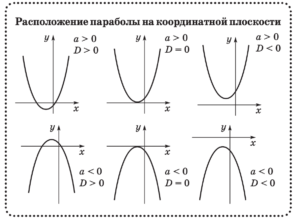
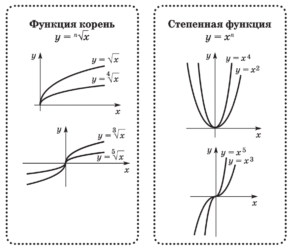
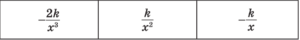Функции. Свойства функций

Графики элементарных функций

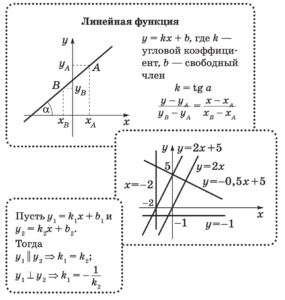
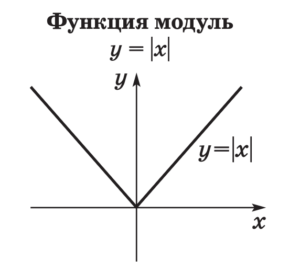
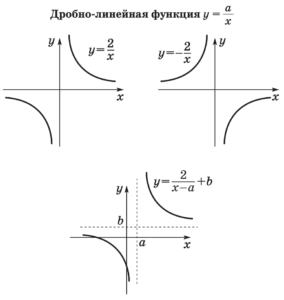
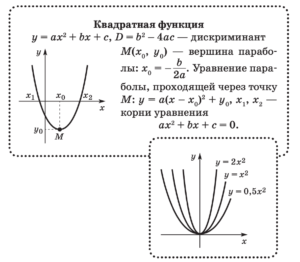
Свойства элементарных функций
Чтение функции по изображённому графику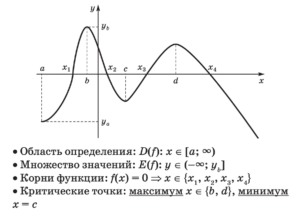

Исследование функций с помощью производной

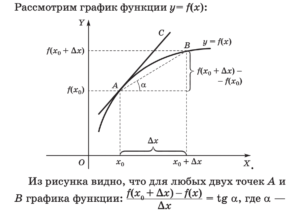
Для решения задачи на производную достаточно знать, что значение производной функции в данной точке равно тангенсу угла, который касательная к графику, проведённая в этой точке, образует с поло- жительным направлением оси абсцисс.

Кроме того, нужно знать, что:

• в каждой точке интервала возрастания дифференцируемой на этом интервале функции её производная неотрицательная;
• в каждой точке интервала убывания дифференцируемой на этом интервале функции её производная неположительная;
• в каждой точке экстремума производная либо равна нулю, либо не существует («угол» на графике функции).

Обратно, если дан график производной функции, то:

• на тех интервалах, где он расположен выше оси абсцисс (т. е. производная положительна), функция возрастает; на тех интервалах, где он расположен ниже оси абсцисс (т. е. производная отрицательна), функция возрастает;
• на тех интервалах, где он расположен ниже оси абсцисс (т. е. производная отрицательна), функция убывает.

Общие точки графика производной и оси абсцисс (т. е. точки, в которых производная равна нулю) либо являются точками максимума, если график производной пересекает ось абсцисс «сверху вниз» (т. е. производная меняет знак с плюса на минус: возрастание функции сменяется убыванием), либо являются точками минимума, если график производной пересекает ось абсцисс «снизу вверх» (т. е. производная меняет знак с минуса на плюс: убывание функции сменяется возрастанием), либо не являются точками экстремума (график производной не пересекает ось абсцисс, а лишь касается её; в этом случае не происходит смены знака производной и характер монотонности функции не меняется).

Применение производной к исследованию функции

Производная широко используется для исследования функций, т.е. для изучения различных свойств функций. Например, с помощью производной можно находить промежутки возрастания и убывания функции, её наибольшие и наименьшие значения.

Возрастание и убывание функции

• Функцию y = f(x) называют возрастающей на промежутке, если для любых x1 и x2, принадлежав- ших этому промежутку, из условия x1 < x2 cледует, что f(x1) < f(x2).
• Функцию y = f(x) называют убывающей на про- межутке, если для любых x1 и x2, принадлежавших этому промежутку, из условия x1 < x2 следует, что f(x1) > f(x2).
• Если f'(x) > 0 на промежутке, то функция y = f(x) возрастает на этом промежутке.
• Если fc(x) < 0 на промежутке, то функция y = f(x) убывает на этом промежутке.

Схема отыскания промежутков возрастания и убывания функции:

• находим область определения заданной функ- ции y = f(x);
• вычисляем производную f'(x) функции y = f(x);
• решаем неравенство:

f'(x) ≥ 0 — находим промежутки возрастания функции y = f(x);

f'(x) ≤ 0 — находим промежутки убывания функции y = f(x).

Экстремумы функции

• Если производная левее стационарной точки положительна, а правее — отрицательна, т.е. при переходе через стационарную точку производная меняет знак с «+» на «–», то эта стационарная точка является точкой экстремума-максимума.
• Если при переходе через стационарную точку производная меняет знак с «–» на «+», то эта ста- ционарная точка является точкой экстремума-ми- нимума.
• Если при переходе через стационарную точку производная сохраняет знак или «–» или «+», то эта стационарная точка является точкой экстрему- ма-перегиба.
  

  Геометрический смысл производной

  Уравнение касательной

  Применение первообразной