Геометрия. Планиметрия

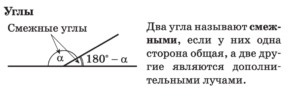
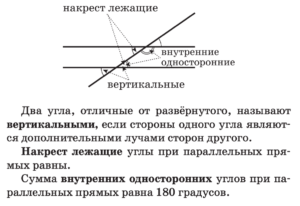
Треугольники

Общие свойства треугольника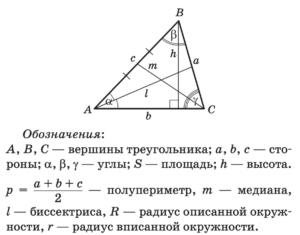

Основные соотношения в треугольнике

Соотношения между сторонами и угламиПлощадь треугольника

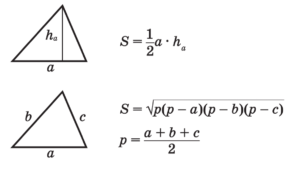
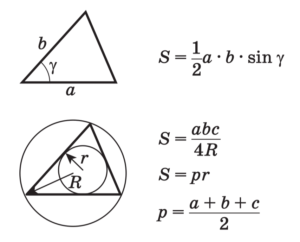
Специальные виды треугольников

Прямоугольный треугольник — треугольник у которого один из углов прямой.

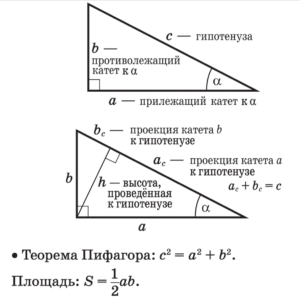
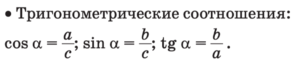
Равносторонний треугольник — треугольник, у которого все стороны равны.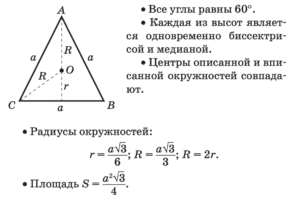Медиана, биссектриса, средняя линия треугольника

Медиана — отрезок, соединяющий вершину треугольника с серединой противоположной стороны.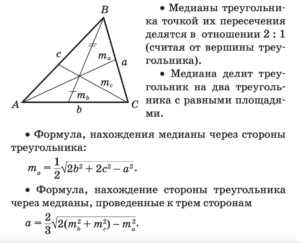Средняя линия — отрезок, соединяющий середины двух сторон треугольника.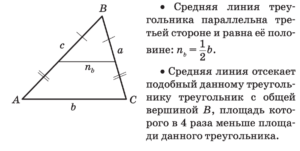

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону).

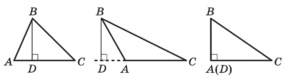
В зависимости от типа треугольника высота BD может содержаться:

• внутри треугольника — это для остроугольного треугольника,
• совпадать с его стороной, т. е. являться катетом прямоугольного треугольника;
• проходить вне треугольника у тупоугольного треугольника.

Биссектриса — луч, выходящий из вершины треугольника и делящий угол пополам.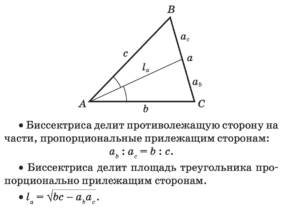Четырёхугольники. Многоугольники

Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельные.

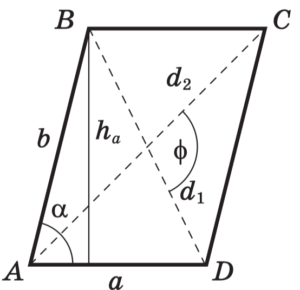
Ромб — параллелограмм, все стороны которого равны.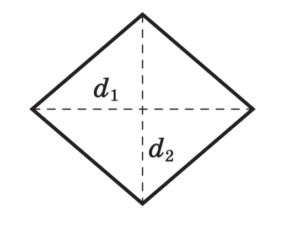Квадрат — прямоугольник, у которого все стороны равны.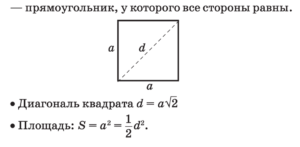Трапеция — четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.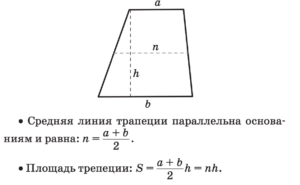

Произвольный выпуклый четырёхугольник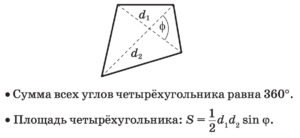Произвольный выпуклый многоугольник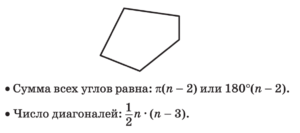

Правильный многоугольник — многоугольник, у которого все стороны и углы равны между собой.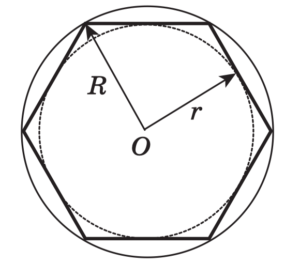Окружность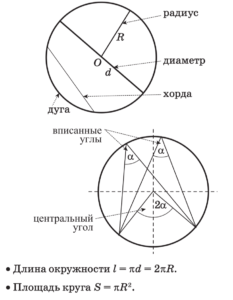Свойства хорды

Хорда — отрезок, соединяющий две точки окружности.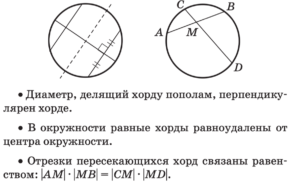

Свойства касательной и секущей

Касательная — прямая, имеющая с окружностью одну общую точку.

Секущая — прямая, имеющая с окружностью две общие точки.

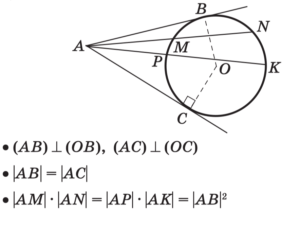Свойства сектора

Сектор — часть круга, ограниченная двумя его радиусами.Свойства описанной окружности

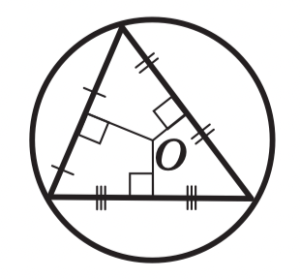Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трём сторонам.

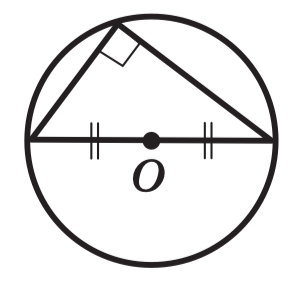Центр окружности, описанной около
прямоугольного треугольника, лежит на середине гипотенузы.

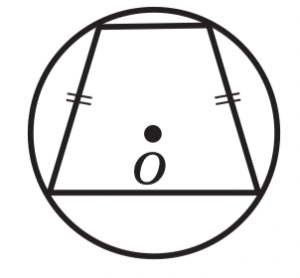Около трапеции можно описать окружность только тогда, когда трапеция равнобокая.

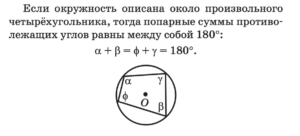Свойства вписанной окружности

Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.

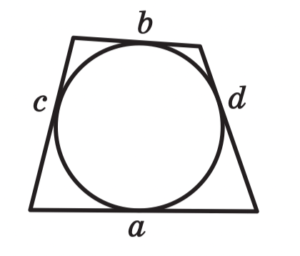
Если окружность вписана в произвольный четырёхугольник, тогда попарные суммы противолежащих сторон равны между собой: a + b = c + d.